图

图由顶点集和边集组成，即， $G = (V, E)$

$V$ 是顶点的集合，顶点代表数据元素
$E$ 是连接顶点的边的集合，边代表元素间的关系

根据边的方向性，可将图分为有向图和无向图

有向图：边有方向，边用 <> 表示，例如， <A, B> 表示从 A 出发到 B 的一条边
无向图：边无方向，用 () 表示，例如， (A, B) 表示顶点 A 和 B 之间有一条边

另外，可以根据顶点之间的关系为边设置权重

加权图：边被赋予一个权值 W
加权有向图：边表示为 <A, B, W>
加权无向图：边表示为 (A, B, W)

# 图的操作

基本操作：

构造一个由若干个节点、0 条边组成的图
判断两个节点之间是否有边存在
在图中添加或删除一条边
返回图中的节点数或边数
按某种规则遍历图中的所有节点

一些与应用密切关联的操作

拓扑排序
关键路径
找最小生成树
找最短路径等

# 图的抽象类

以加权有向图为例

	template <class TypeOfVer, class TypeOfEdge> // 数据元素的类型 TypeOfVer ，边的权值的类型 TypeOfEdge
	class graph {
	public:
	virtual void insert(TypeOfVer x, TypeOfVer y, TypeOfEdge w) = 0;
	virtual void remove(TypeOfVer x, TypeOfVer y) = 0;
	virtual bool exist(TypeOfVer x, TypeOfVer y) const = 0;
	virtual ~graph() {}
	int numOfVer() const {return Vers;}
	int numOfEdge() const {return Edges;}

	protected:
	int Vers, Edges;
	};

# 图的术语

度：图中连接于某一节点的边的总数

入度：有向图中进入某一节点的边数
出度：有向图中离开某一节点的边数

子图：设 $G = (V, E)$ 和 $G' = (V', E')$ ，若 $V' \subset V$ 且 $E' \subset E$ ，则称 $G'$ 是 $G$ 的子图

路径：顶点的序列

简单路径：如果一条路径上的所有节点，除了起始节点和终止节点可能相同外，其余的节点都不相同
环：环是一条简单路径，其起始节点和终止节点相同，且路径长度至少为 1

路径长度

非加权的路径长度：组成路径的边数
加权路径长度：路径上所有边的权值之和

连通性：两点之间存在路径

无向图
- 连通：顶点 $v$ 至 $v'$ 之间有路径存在
- 连通图：任意两点之间都连通的无向图，例如，左下图是一个连通图，右下图不是
- 连通分量：非连通图中的极大连通子图，例如，右下图的两个红圈就是连通分量

左侧是连通图，右侧是非连通图

有向图
- 强连通图：顶点 $v$ 至 $v'$ 之间有路径存在，例如，左下图是一个强连通图，右下图不是
- 强连通分量：非强连通图中的极大连通子图，例如，右下图的三个红圈就是连通分量
- 弱连通图：如有向图 $G$ 不是强连通的，但如果把它看成是无向图时是连通的，则它是一个弱连通图，例如右下图

左侧是强连通图，右侧是弱连通图

完全图

无向完全图：任意两个节点之间都有边的无向图，例如左下图
有向完全图：任意两个节点之间都有弧的有向图，例如右下图

左侧是无向完全图，右侧是有向完全图

生成树：连通图的极小连通子图，如下图中右侧两图就是左图的生成树

包含图的所有 $n$ 个节点和 $n - 1$ 条边
在生成树中添加一条边之后，必定会形成回路或环

生成树

最小生成树：加权无向图的所有生成树中边的权值和最小的生成树，如下图中右图就是左图的最小生成树

最小生成树

# 图的存储

图的顶点集合 $V$ 存储在一个数组或者链表中

边的集合的表示方式通常有两种

邻接矩阵
邻接表

# 邻接矩阵

边的集合 $E$ 用一个 $n \times n$ 的矩阵表示

对于有向图，如果 $i$ 至 $j$ 存在有向边， $A[i, j] = 1$ ；如果不存在有向边， $A[i, j] = 0$

节点 $i$ 的出度：第 $i$ 行元素之和
节点 $j$ 的入度：第 $j$ 列元素之和

有向图的邻接矩阵

对于无向图，如果 $i$ 至 $j$ 存在一条边， $A[i, j] = 1$ ；如果不存在一条边， $A[i, j] = 0$

矩阵 $A$ 是一个对称矩阵
节点 $i$ 的度：第 $i$ 行或者第 $i$ 列元素之和

无向图的邻接矩阵

对于加权图，如果 $i$ 至 $j$ 有一条边并且权值为 $a$ ，则 $A[i, j] = 1$ ；如果 $i$ 至 $j$ 没有边，则 $A[i, j]$ 为空或其他标志（例如，定义为正无穷 $+ \infty$ ）

加权图的邻接矩阵

性能分析

优点：基本操作都是 $O(1)$ 的时间复杂度，不仅能找到出发的边，也能找到到达的边
缺点：即使边的数量远小于 $n^2$ ，也需 $n^2$ 个单元的内存（大多数的图的边数都远小于 $n^2$ ）

# 邻接表

邻接表是图的标准存储方式

顶点集合 $V$ ：用数组或单链表的形式存放所有的节点值，如果节点数 $n$ 固定，则采用数组形式，否则可采用单链表的形式

边集合 $E$ ：同一个节点出发的所有边组成一个单链表

如果是加权图，单链表的每个节点中还要保存权值

邻接表

优点：

内存 = 节点数 + 边数
处理时间：节点数 + 边数，即， $O(\vert V \vert + \vert E \vert )$

缺点：

确定从 $i$ 到 $j$ 是否有边，最坏需要 $O(n)$ 的时间复杂度
有向图中寻找进入某节点的边，非常困难
无向图同一条边表示两次，边表空间浪费一倍

# 链式前向星

邻接表通过一条链表来记录每个顶点的所有邻边，然而，这些邻边之间是没有逻辑关系的（前后关系）

前向星可以让每个顶点的所有邻边具有逻辑关系：如果知道某个顶点的第一条边，就可以知道这个顶点的所有邻边

	// 建立边结构体
	struct Edge {
	int w; // 边的权值
	int to; // 边的终点
	int next; // 同起点的下一条边的的编号
	};

	Edge edges[N]; // N 为边的条数（针对无向图中的边 u -- v，需添加两条相反的边）
	//edges [i].to 表示第 i 条边的终点
	//edges [i].next 表示与第 i 条边同起点的下一条边的编号
	//edges [i].w 表示第 i 条边的权值

	vector<int> head(N, -1); //head [i] 表示以 i 为起点的第一条边的编号
	// 也可以理解成：以 i 为起点的编号最大的边，因为前向星是使用的头插法，在最前面的就是最后插入的边

	int cnt = 0;

	void add(int u, int v, int w) { // 添加一条起点为 u 、终点为 v 、权值为 w 的边
	edges[cnt].w = w;
	edges[cnt].to = v;
	edges[cnt].next = head[u];
	head[u] = cnt++;
	}

	// 遍历（遍历是逆序的）
	for (int j = head[i]; j != -1; j = edge[j].next) { // 输出节点 i 的所有邻居节点
	cout << edges[j].to << endl;
	}

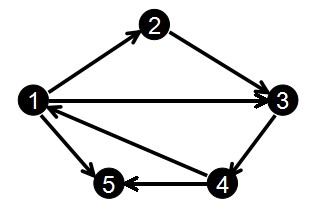
以下图为例

依次输入边的起点和终点：

对应 edges 和 head 数组的变化如下：

edge[0].to = 2;     edge[0].next = -1;      head[1] = 0;
edge[1].to = 3;     edge[1].next = -1;      head[2] = 1;
edge[2].to = 4;     edge[2],next = -1;      head[3] = 2;
edge[3].to = 3;     edge[3].next = 0;       head[1] = 3;
edge[4].to = 1;     edge[4].next = -1;      head[4] = 4;
edge[5].to = 5;     edge[5].next = 3;       head[1] = 5;
edge[6].to = 5;     edge[6].next = 4;       head[4] = 6;

参考：深度理解链式前向星

# 其他方法

逆邻接表：将进入同一节点的边组织成一个单链表

逆邻接表

十字链表：既记录前驱又记录后继，而且每条边只存储一次

十字链表

邻接多重表：解决无向图中边存储两次的问题。每个边的链表节点中存储与这条边相关的两个顶点，以及分别依附于这两个顶点下一条的边

邻接多重表

参考：青舟智学：图的定义与存储

# 图的遍历

# 深度优先遍历

# 广度优先遍历

# 欧拉回路

图