# LeetCode 100. 相同二叉树

100. Same Tree

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

• 两棵树上的节点数目都在范围 $[0, 100]$ 内
• $-10^4 \le$ Node.val $\le 10^4$

# 思路

如果两棵树的所有节点都相同，则这两棵二叉树相同

因此，判断两棵二叉树是否相同的步骤可分为：

• 判断根节点的值是否相等
• 判断左子树是否相同
• 判断右子树是否相同

解法类似于 LeetCode 101. 对称二叉树

# Method 1: 递归

算法思路：

1. 定义递归函数：检查以 p 、 q 为根节点的两棵是否相同

2. 递归函数的内部，做以下判断：

   • 若 p 与 q 同时为空，则两树相同
   • 若 p 与 q 不同时为空，则两树不同
   • 若 p 与 q 的值不相等，则两树相同
   • 若 p 的左子树 与 q 的左子树不相同，则两树不同
   • 若 p 的右子树 与 q 的右子树不相同，则两树不同

代码实现：

bool isSameTree(TreeNode* p, TreeNode* q) {

    if (!p && !q) return true;

    if (!p || !q) return false;

    if (p->val != q->val) return false;

    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);

}

时间复杂度：$O(\min(m, n))$，其中，$m$, $n$ 分别是两棵二叉树的节点数

空间复杂度：$O(\min(m, n))$，这里考虑了递归使用的栈空间

• 递归调用的层数不会超过较小的二叉树的最大高度
• 最坏情况下，二叉树的高度等于节点数

# Method 2: 迭代

本题也可以使用迭代法来显式地维护 Method 1 中调用的栈

这里利用 栈 来存放待访问的节点（也可以使用队列，区别仅在于节点的访问顺序）

# 写法一

类似于 LeetCode 101. 对称二叉树 的 Method 2

代码实现：

bool isSameTree(TreeNode* p, TreeNode* q) {

    stack<TreeNode*> stk;

    stk.push(q);

    stk.push(p);

    TreeNode *u = nullptr, *v = nullptr;

    while (!stk.empty()) {

        u = stk.top();

        stk.pop();

        v = stk.top();

        stk.pop();

        if ((u == nullptr) && (v == nullptr)) continue;

        if ((u == nullptr) || (v == nullptr)) return false;

        if (u->val != v->val) return false;

        stk.push(v->right);

        stk.push(u->right);

        stk.push(v->left);

        stk.push(u->left);

    }

    return true;

}

若采用 队列 来实现迭代法，将上述代码中的 栈（及其成员函数）替换为 队列（及其成员函数）即可

# 写法二

为降低算法复杂度，可以仅将非空节点入栈

因此，在将两棵树的子节点入栈前，须对两棵树的结构进行判断

算法思路：

1. 定义一个栈，若 p 与 q 非空，将其入栈
2. 执行循环，直到栈为空：
   • 从栈中取出两个节点，记作 u 和 v
   • 判断 u 和 v 的值是否相等
   • 判断 u 的右子节点 和 v 的右子节点 是否为空
     • 如果有且仅有一个为空，则说明 u 和 v 的右子树结构不同，返回 false
     • 如果均不为空，则将其入栈，以进一步判断右子树是否相同
   • 判断 u 和 v 的左子节点是否为空，类似于上一步
3. 循环结束时，栈为空，且不存在不相同的节点，返回 true

其中，当 u 和 v 的右子节点均为空时，对应的右子树相同，无需再将其入栈，类似地，当 u 和 v 的左子节点均为空时，也无需将其入栈

代码实现：

bool isSameTree(TreeNode* p, TreeNode* q) {

    if (!p && !q) return true;

    if (!p || !q) return false;

    stack<TreeNode*> stk;

    stk.push(q);

    stk.push(p);

    TreeNode *u = nullptr, *v = nullptr;

    while (!stk.empty()) {

        u = stk.top();

        stk.pop();

        v = stk.top();

        stk.pop();

        if (u->val != v->val) return false;

        if ((u->right == nullptr) ^ (v->right == nullptr)) //u 或 v 不存在右子节点

            return false;

        if ((u->left == nullptr) ^ (v->left == nullptr))   //u 或 v 不存在左子节点

            return false;

        if (v->right) stk.push(v->right); // 将非空的右子节点入栈

        if (u->right) stk.push(u->right);

        if (v->left) stk.push(v->left);   // 将非空的左子节点入栈

        if (u->left) stk.push(u->left);

    }

    return true;

}

时间复杂度：$O(\min(m, n))$，其中，$m$, $n$ 分别是两棵二叉树的节点数

空间复杂度：$O(\min(m, n))$

参考：力扣官方题解：相同的树

# LeetCode 101. 对称二叉树

LeetCode 101. Symmetric Tree

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 $[1, 1000]$ 内
• $-100 \le$ Node.val $\le 100$

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

# 思路

如果一棵树的左子树与右子树对称，那么这棵树就是对称的

进一步地分析，子树 A1 与子树 A2 对称，需要满足以下条件：

• A1 的根节点值 等于 A2 的根节点值
• A1 的左子树 与 A2 的右子树 对称
• A1 的右子树 与 A2 的左子树 对称

如下图所示，检查二叉树对称性的步骤可分为：

• 检查 B 与 C 的值是否相等
• 检查 D 与 G 的值是否相等
• 检查 E 与 F 的值是否相等

# Method 1: 递归

算法思路：

1. 定义一个递归函数，函数传入两个参数：

   • 指针 l ：指向左侧的子树 A1
   • 指针 r ：指向右侧的子树 A2

2. 递归函数的作用：检查子树 A1 与 A2 是否对称

3. 递归函数的内部，做以下判断：

   • 若 l 与 r 同时为空，则 A1 与 A2 对称
   • 若 l 与 r 不同时为空，则 A1 与 A2 不对称
   • 若 l 与 r 的值不相等，则 A1 与 A2 不对称
   • 若 l 的左子树 与 r 的右子树不对称，则 A1 与 A2 不对称
   • 若 l 的右子树 与 r 的左子树不对称，则 A1 与 A2 不对称

代码实现：

bool check(TreeNode* l, TreeNode* r) {  // 检查 l 与 r 及其子树是否对称

    if (l == nullptr && r == nullptr) return true;  //l 与 r 均为空

    if (l == nullptr || r == nullptr) return false; //l 为空，或，r 为空

    if (l->val != r->val) return false; // 检查 l 与 r 是否对称

    return check(l->left, r->right) && check(l->right, r->left); // 检查 l 与 r 的子树是否对称

}

bool isSymmetric(TreeNode* root) {

    if (root == nullptr) return true;

    return check(root->left, root->right);

}

时间复杂度：$O(n)$，其中，$n$ 为二叉树的节点数

空间复杂度：$O(\log{n})$，这里考虑了递归使用的栈空间

# Method 2: 迭代

对于二叉树的前序、中序、后序遍历，我们可以使用迭代法来显式地维护递归调用的栈

类似地，本题可以定义一个 队列 来显式地维护 Method 1 中递归调用的栈，以检查两棵子树的对称性

这里为了能够逐层遍历，采用的是 队列 来实现迭代法，事实上，也可以使用 栈 来实现

算法流程：

1. 定义一个队列，并将根节点 root 的两个子节点入队
2. 执行循环，直到队列为空：
   • 从队列中取出两个节点，记作 u 和 v （类似于 Method 1 中的 指针 l 和 r ，分别指向子树 A1 和 A2）
   • 若 u 和 v 均为空，则跳过本次循环
   • 若 u 和 v 中有且仅有一个为空，则子树不对称，返回 false
   • 若 u 和 v 均不为空，判断 u 与 v 的值是否相等，若不相等，则返回 false
   • 将 u 的左子节点、 v 的右子节点依次入队
   • 将 u 的右子节点、 v 的左子节点依次入队
3. 循环结束时，队列为空，不存在不对称的子树，返回 true

代码实现：

bool isSymmetric(TreeNode* root) {

    if (root == nullptr) return true;

    queue<TreeNode*> que;

    que.push(root->left);

    que.push(root->right);

    TreeNode *u = new TreeNode(0), *v = new TreeNode(0);

    while (!que.empty()) {

        u = que.front();    // 指向子树 A1

        que.pop();

        v = que.front();    // 指向子树 A2

        que.pop();

        if (!u && !v) continue;             // A1 与 A2 同时为空

        if (!u || !v) return false;         // A1 与 A2 不同时为空

        if (u->val != v->val) return false; // A1 与 A2 的根节点值不相等

        que.push(u->left);  // A1 的左子树

        que.push(v->right); // A2 的右子树

        que.push(u->right); // A1 的右子树

        que.push(v->left);  // A2 的左子树

    }

    return true;

}

时间复杂度：$O(n)$，其中，$n$ 为二叉树的节点数

空间复杂度：$O(n)$

# LeetCode 102. 二叉树的层序遍历

LeetCode 102. Binary Tree Level Order Traversal

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 $[0, 2000]$ 内
• $-1000 \le$ Node.val $\le 1000$

# 思路

逐层遍历二叉树，其中，每层按从左到右顺序遍历

由于队列具有先进先出特性，本题可利用队列来存放 待访问的节点，即，按从左到右的顺序将待访问的节点依次加入到队列中

注意本题要求输出一个二维数组，其中，二维数组中的每一个一维数组，表示 二叉树每一层上所有节点的值。因此，一维数组的长度 即为 对应层上的二叉树节点数，亦为 上一层访问结束后的队列长度

# Method: 广度优先搜索

算法思路：

1. 将根节点入队

2. 当队列不为空，执行以下循环：

   • 求当前队列的长度 $s_i$
   • 依次从队列中取 $s_i$ 个元素：
     • 读取其值，将值临时存放到一维数组 tmp 中
     • 将非空的左、右子节点依次入队
   • 将一维数组 tmp 添加到目标数组 res

普通的广度优先搜索每次只取 1 个元素拓展，而这里每次取 $s_i$ 个元素，即，第 $i$ 次迭代就得到了二叉树的第 $i$ 层的 $s_i$ 个元素

代码实现：

vector<vector<int>> levelOrder(TreeNode* root) {

    vector<vector<int>> res;

    queue<TreeNode*> que; // 队列存放的是待展开的二叉树节点

    if (root != nullptr) que.push(root);

    while (!que.empty()) {

        vector<int> tmp;

        int size = que.size();

        for (int i = 0; i < size; i++) {

            TreeNode* node = que.front();

            que.pop();

            tmp.push_back(node->val);

            if (node->left != nullptr) que.push(node->left);

            if (node->right != nullptr) que.push(node->right);

        }

        res.push_back(tmp);

    }

    return res;

}

时间复杂度：$O(n)$，每个点入队出队各一次，其中 $n$ 为树的所有节点的个数

空间复杂度：$O(n)$，队列中元素的个数不超过 $n$ 个

代码随想录：二叉树的层序遍历

# LeetCode 104. 二叉树的最大深度

LeetCode 104. Maximum Depth of Binary Tree

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 二叉树的节点数在范围 $[0, 10^4]$ 内
• $-100 \le$ Node.val $\le 100$

# 思路

二叉树的深度是从上往下数，而高度是从下往上数

即，按前序遍历顺序求的是二叉树的深度，按后序遍历顺序求的是二叉树的高度。具体可参考 LeetCode 110. 平衡二叉树 中的概念辨析

# Method 1: 递归

本题可通过后序遍历来计算根节点的高度，从而得到二叉树的最大深度（根节点的高度，即为二叉树的最大深度）

算法思路：

• 若已知左子树和右子树的高度分别为 $l$ 和 $r$ ，则二叉树的高度为 $1 + \max{(l, r)}$

• 左子树与右子树的高度可通过同样方式获得，即，递归

• 递归的终止条件为：节点为空

代码实现：

int maxDepth(TreeNode* root) {

    if (root == nullptr) return 0; // 当 root 为空时，深度为 0

    int l = maxDepth(root->left);  // 左子树的高度

    int r = maxDepth(root->right); // 右子树的高度

    int ans = 1 + max(l, r);

    return ans;

}

时间复杂度：$O(n)$，其中，$n$ 为二叉树的节点数

空间复杂度：$O(h)$，其中，$h$ 为二叉树的最大深度（这里考虑了递归所需的栈空间）

本题也可以使用前序遍历计算节点的深度，节点深度的最大值即为二叉树的最大深度。具体可参考 代码随想录：二叉树的最大深度

# Method 2: 层序遍历

算法思路：

• 利用队列存储待访问的节点，与 LeetCode 102. 二叉树的层序遍历 类似
• 逐层遍历，遍历的层数就是二叉树的最大深度（即，从根节点到最底层节点所经历的层数）

代码实现：

int maxDepth(TreeNode* root) {

    int ans = 0; // 二叉树的深度

    queue<TreeNode*> que;

    if (root) que.push(root);

    while (!que.empty()) {

        int size = que.size();

        for (int i = 0; i < size; i++) {

            TreeNode* tmp = que.front();

            que.pop();

            if (tmp->left) que.push(tmp->left);

            if (tmp->right) que.push(tmp->right);

        }

        ans++;

    }

    return ans;

}

时间复杂度：$O(n)$，其中，$n$ 为二叉树的节点数

空间复杂度：$O(n)$

参考：力扣官方题解：二叉树的最大深度

# LeetCode 559. N 叉树的最大深度

LeetCode 559. Maximum Depth of N-ary Tree

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：3

示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：5

提示：

• 树的深度不超过 $10^4$
• 树的节点数在范围 $[0, 10^4]$ 内

# Method 1: 递归

代码实现：

int maxDepth(Node* root) {

    if (!root) return 0;

    int depth = 0;

    for (int i = 0; i < root->children.size(); i++) {

        int temp = maxDepth(root->children[i]); // 第 i 棵子树的最大深度

        depth = max(depth, temp); // 所有子树的最大深度

    }

    return 1 + depth;             // 以 root 为根节点的树的最大深度

}

时间复杂度：$O(n)$，其中，$n$ 为 N 叉树的节点数

空间复杂度：$O(h)$，其中，$h$ 为 N 叉树的最大深度（这里考虑了递归所需的栈空间）

# Method 2: 层序遍历

代码实现：

int maxDepth(Node* root) {

    int depth = 0;

    queue<Node*> que;

    if (root) que.push(root);

    while (!que.empty()) {

        depth++;

        int size = que.size();

        for (int i = 0; i < size; i++) {

            Node* tmp = que.front();

            que.pop();

            for (int j = 0; j < tmp->children.size(); j++)

                if (tmp->children[j]) que.push(tmp->children[j]);

        }

    }

    return depth;

}

时间复杂度：$O(n)$，其中，$n$ 为 N 叉树的节点数

空间复杂度：$O(n)$

# LeetCode 105. 从前序与中序遍历序列构造二叉树

105. Construct Binary Tree from Preorder and Inorder Traversal

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1：

输入：preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出：[3,9,20,null,null,15,7]

示例 2：

输入：preorder = [-1], inorder = [-1]
输出：[-1]

提示：

• $1 \le$ preorder.length $\le 3000$
• inorder.length == preorder.length
• $-3000 \le$ preorder[i] , inorder[i] $\le 3000$
• preorder 和 inorder 均无重复元素
• inorder 的每个元素均出现在 preorder
• preorder 保证为二叉树的前序遍历序列
• inorder 保证为二叉树的中序遍历序列

# 思路

根据前序遍历数组的第一个元素来确定根节点

在中序遍历数组中找到根节点，根节点左侧、右侧分别为左子树、右子树的中序遍历序列

根据左子树的中序遍历序列长度，确定左子树、右子树的前序遍历序列

• 树的中序遍历序列长度等于前序遍历序列长度，并且同一棵树的节点在遍历数组中连续

依此类推，最终可确定每个节点的左、右子节点

# Method: 递归

算法思路：类似于 LeetCode 106. 从中序与后序遍历序列构造二叉树

分割数组时，坚持区间不变量原则，左闭右开，或者左闭右闭

代码实现：

TreeNode* traversal(vector<int>& preorder, vector<int>& inorder, int preorderBegin, int preorderEnd, int inorderBegin, int inorderEnd) {

    if (preorderBegin == preorderEnd) return nullptr;

    // 根节点

    int rootValue = preorder[preorderBegin];

    TreeNode *root = new TreeNode(rootValue);

    // 中序遍历分界线

    int delimiterIndex = inorderBegin;

    for (; delimiterIndex < inorderEnd; delimiterIndex++)

        if (inorder[delimiterIndex] == rootValue) break;

    // 左子树的节点数

    int leftSize = delimiterIndex - inorderBegin;

    // 左子树的前序区间：[preorderBegin + 1, preorderBegin + 1 + leftSize) 

    // 左子树的中序区间：[inorderBegin, delimiterIndex)

    root->left = traversal(preorder, inorder, preorderBegin + 1, preorderBegin + 1 + leftSize, inorderBegin, delimiterIndex);

    // 右子树的前序区间：[preorderBegin + 1 + leftSize, preorderEnd)

    // 右子树的中序区间：[delimiterIndex + 1, inorderEnd)

    root->right = traversal(preorder, inorder, preorderBegin + 1 + leftSize, preorderEnd, delimiterIndex + 1, inorderEnd);

    return root;

}

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {

    return traversal(preorder, inorder, 0, preorder.size(), 0, inorder.size());

}

时间复杂度：$O(n^2)$，其中 $n$ 为二叉树的节点数

• 每个节点都将调用一次 traversal 函数，时间复杂度为 $O(n)$
• 每次调用 traversal 函数时，需要找到根节点在中序遍历数组中的位置
  • 平均情况下，时间复杂度为 $O(\log{n})$
  • 最坏情况下，时间复杂度为 $O(n)$

# 优化

可以考虑使用哈希表来快速定位根节点在中序遍历数组中的位置

• key 表示一个元素（节点的值）， value 表示其在中序遍历序列中的出现位置

具体实现：

1. 定义全局变量

   unordered_map<int, int> index;

2. 在 buildTree 函数中，构造哈希映射

   	for (int i = 0; i < n; ++i) {
   	index[inorder[i]] = i;
   	}

3. 在递归函数 traversal 中，使用哈希表查询根节点

   int delimiterIndex = index[preorder[preorderBegin]]; //preorder 首元素为根节点的值

优化后的算法时间复杂度为 $O(n)$

参考：力扣官方题解：从前序与中序遍历序列构造二叉树

# LeetCode 106. 从中序与后序遍历序列构造二叉树

106. Construct Binary Tree from Inorder and Postorder Traversal

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1：

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2：

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示：

• $1 \le$ inorder.length $\le 3000$
• postorder.length == inorder.length
• $-3000 \le$ inorder[i] , postorder[i] $\le 3000$
• inorder 和 postorder 均无重复元素
• postorder 的每个元素均出现在 inorder
• inorder 保证为二叉树的中序遍历序列
• postorder 保证为二叉树的后序遍历序列

# 思路

根据后序遍历的最后一个元素来确定根节点

在中序遍历中找到根节点，得到左子树的中序遍历、右子树的中序遍历

• 依据：在中序遍历的数组中，根节点左侧为左子树，右侧为右子树

在后序遍历中分别找到左子树所有节点、右子树所有节点，即可得到左子树、右子树的后序遍历

• 依据：后序遍历的数组大小等于中序的数组大小，同一棵树的节点在遍历数组中连续

依此类推，最终可确定每个节点的左、右子节点

# Method: 递归

算法流程：

• 若二叉树的中序遍历数组为空，当前树为空

• 若不为空，取后序数组的最后一个元素作为根节点

• 找到根节点在中序数组的位置，作为切割点

• 切割中序数组，分成中序左数组、中序右数组

• 根据中序左数组、中序右数组的大小来切割后序数组，将其分成后序左数组、后序右数组

• 递归处理左子树和右子树

分割数组时，坚持区间不变量原则，左闭右开，或者左闭右闭

为降低时空间复杂度，通过使用左子树、右子树节点在数组 inorder 和 postorder 的下标索引，表示左子树、右子树的中序、后序遍历的结果数组

代码实现：

// 根据中序区间和后序区间确定根节点及左右子树

// 中序区间 [inorderBegin, inorderEnd)，后序区间 [postorderBegin, postorderEnd)

TreeNode* traversal(vector<int> &inorder, vector<int> &postorder, int inorderBegin, int inorderEnd, int postorderBegin, int postorderEnd) {

    if (inorderBegin == inorderEnd) return nullptr;  // 空数组，二叉树为空

    int rootValue = postorder[postorderEnd - 1];     // 后序遍历的最后一个元素为根节点

    TreeNode *root = new TreeNode(rootValue);        // 根节点

    if (inorder.size() == 1) return root;

    // 找到根节点在中序遍历数组中的位置，即，左、右子树的分界线

    int delimiterIndex;

    for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd ; delimiterIndex++) {

        if (inorder[delimiterIndex] == rootValue) break;

    }

    // 切割中序数组

    // 左子树的中序遍历数组，对应在 inorder 中的索引为 [leftInorderBegin, leftInorderEnd)

    int leftInorderBegin = inorderBegin;

    int leftInorderEnd = delimiterIndex;

    // 右子树的中序遍历数组，对应在 inorder 中的索引为 [rightInorderBegin, rightInorderEnd)

    int rightInorderBegin = delimiterIndex + 1; // 需排除根节点

    int rightInorderEnd = inorderEnd;

    // 切割后序数组

    // 左子树的后序遍历数组，对应在 postorder 中的索引为 [leftPostorderBegin, leftPostorderEnd)

    int leftPostorderBegin = postorderBegin;

    int leftPostorderEnd = postorderBegin + (leftInorderEnd - leftInorderBegin);

    // 右子树的后序遍历数组，对应在 postorder 中的索引为 [rightPostorderBegin, rightPostorderEnd)

    int rightPostorderBegin = postorderBegin + (leftInorderEnd - leftInorderBegin);

    int rightPostorderEnd = postorderEnd - 1; // 需排除根节点

    // 递归到左子树（确定 root 的左子节点指针）

    root->left = traversal(inorder, postorder, leftInorderBegin, leftInorderEnd, leftPostorderBegin, leftPostorderEnd);

    // 递归到右子树（确定 root 的右子节点指针）

    root->right = traversal(inorder, postorder, rightInorderBegin, rightInorderEnd, rightPostorderBegin, rightPostorderEnd);

    return root;

}

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {

    if (inorder.size() == 0) return nullptr;

    return traversal(inorder, postorder, 0, inorder.size(), 0, postorder.size());

}

时间复杂度：$O(n^2)$，其中 $n$ 为二叉树的节点数

• 每个节点都将调用一次 traversal 函数，时间复杂度为 $O(n)$
• 每次调用 traversal 函数时，需要找到根节点在中序遍历数组中的位置
  • 平均情况下，时间复杂度为 $O(\log{n})$
  • 最坏情况下，时间复杂度为 $O(n)$

空间复杂度：$O(n)$，考虑了递归使用的栈空间

参考：代码随想录：从中序与后序遍历序列构造二叉树

简化版：

TreeNode* traversal(vector<int> &inorder, vector<int> &postorder, int inorderBegin, int inorderEnd, int postorderBegin, int postorderEnd) {

    if (inorderBegin == inorderEnd) return nullptr;  // 空数组，二叉树为空

    int rootValue = postorder[postorderEnd - 1];     // 后序遍历的最后一个元素为根节点

    TreeNode *root = new TreeNode(rootValue);        // 根节点

    if (inorder.size() == 1) return root;

    // 找到根节点在中序遍历数组中的位置

    int delimiterIndex;

    for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd ; delimiterIndex++)

        if (inorder[delimiterIndex] == rootValue) break;

    // 左子树节点数

    int leftSize = delimiterIndex - inorderBegin;

    // 递归到左子树

    root->left = traversal(inorder, postorder, inorderBegin, delimiterIndex, postorderBegin, postorderBegin + leftSize);

    // 递归到右子树

    root->right = traversal(inorder, postorder, delimiterIndex + 1, inorderEnd, postorderBegin + leftSize, postorderEnd - 1);

    return root;

}

TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {

    if (inorder.size() == 0) return nullptr;

    return traversal(inorder, postorder, 0, inorder.size(), 0, postorder.size());

}

# 优化

另外，可以考虑使用哈希表来快速定位根节点

• key 表示一个元素（节点的值）， value 表示其在中序遍历序列中的出现位置
• 在调用递归函数前，先对中序遍历序列进行一遍扫描，构造出哈希表
• 以后只需要 $O(1)$ 的时间就可以对中序遍历中的根节点进行定位

具体实现：

1. 定义全局变量

   unordered_map<int, int> index;

2. 在 buildTree 函数中构造哈希映射

   	for (int i = 0; i < n; ++i) {
   	index[inorder[i]] = i;
   	}

3. 在递归函数 traversal 中使用哈希表查询根节点

   int delimiterIndex = index[postorder[postorderEnd]]; //postorder 最后元素为根节点的值

优化后的算法时间复杂度为 $O(n)$

参考：力扣官方题解：从中序与后序遍历序列构造二叉树

# LeetCode 107. 二叉树的层序遍历 II

LeetCode 107. Binary Tree Level Order Traversal II

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 $[0, 2000]$ 内
• $-1000 \le$ Node.val $\le 1000$

# 思路

与 LeetCode 102. 二叉树的层序遍历 不同，本题的遍历是从二叉树底层向上遍历

# Method: 广度优先搜索

算法流程：

1. 按照 LeetCode 102. 二叉树的层序遍历 算法自上而下遍历二叉树

2. 反转目标数组

代码实现：

vector<vector<int>> levelOrderBottom(TreeNode* root) {

    vector<vector<int>> res;

    queue<TreeNode*> que;

    if (root) que.push(root);

    while (!que.empty()) {

        int size = que.size();

        vector<int> tmp;

        for (int i = 0; i < size; i++) {

            TreeNode* node = que.front();

            que.pop();

            tmp.push_back(node->val);

            if (node->left) que.push(node->left);

            if (node->right) que.push(node->right);

        }

        res.push_back(tmp);

    }

    reverse(res.begin(), res.end()); // 反转二维数组

    return res;

}

时间复杂度：$O(n)$，其中 $n$ 是二叉树的节点数

空间复杂度：$O(n)$

# LeetCode 108. 将有序数组转换为二叉搜索树

108. Convert Sorted Array to Binary Search Tree

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案

示例 2：

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树

提示：

• $1 \le$ nums.length $\le 104$
• $-104 \le$ nums[i] $\le 104$
• nums 按 严格递增 顺序排列

# 思路

注意本题的数组 nums 为严格递增的有序序列

取数组最中间元素 mid 作为二叉树的根节点， mid 左侧所有元素作为左子树， mid 右侧所有元素作为右子树

于是，左子树所有节点值小于根节点，右子树所有节点值大于根节点，即，满足二叉搜索树的要求

并且，左子树、右子树的最大高度差不超过 1 （当数组元素为偶数时，高度差最大，值为 1），即，满足平衡二叉树的要求

• 若取 mid = left + (right - left) / 2; ，左侧元素个数比右侧少 1
• 若取 mid = left + (right - left + 1) / 2; ，左侧元素个数比右侧多 1

注意：在分割数组时需要坚持不变量原则，即，预先定义有效区间为 左闭右闭 [left, right] （或者 左闭右开 [left, right) ）

由于选择根节点的方式不同，构造出的二叉搜索树也就不同，因此，本题存在多解

# Method: 递归

算法思路：总是选择中间位置左边的数字作为根节点，即，取 mid = left + (right - left) / 2;

这里采用 左闭右闭 原则：从 nums 数组中取出索引为 [left, right] 的所有元素，将其构建为一棵平衡二叉搜索树

代码实现：

TreeNode* buildTree(vector<int> &nums, int left, int right) { // 将数组索引为 [left, right] 的元素建成一棵二叉搜索树

    if (left > right) return nullptr;    // 没有节点需要建立

    int mid = left + (right - left) / 2; // 取 [left, right] 区间中点对应元素值作为根节点值

    TreeNode *node = new TreeNode(nums[mid]);      // 根节点

    node->left = buildTree(nums, left, mid - 1);   // 左子树

    node->right = buildTree(nums, mid + 1, right); // 右子树

    return node;

}

TreeNode* sortedArrayToBST(vector<int>& nums) {

    return buildTree(nums, 0, nums.size() - 1);

}

时间复杂度：$O(n)$，其中 $n$ 是数组的长度

空间复杂度：$O(\log{n})$，递归的最大深度为 $O(\log{n})$

# LeetCode 110. 平衡二叉树

110. Balanced Binary Tree

给定一个二叉树，判断它是否是高度平衡的二叉树。

一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

• 树中的节点数在范围 $[0, 5000]$ 内
• $-10^4 \le$ Node.val $\le 10^4$

# 概念辨析

# 节点的深度与高度

深度是从上往下数，而高度是从下往上数

1. 维基百科

   • 节点的深度：从根节点到该节点路径上的边的条数
   • 结点的高度：从该节点到叶节点路径上的边的条数

2. Leetcode

   • 节点的深度：从根节点到该节点路径上的节点个数
   • 结点的高度：从该节点到叶节点路径上的节点个数

按照维基百科的定义，根节点的深度为 0 ；按照 Leetcode 的定义，根节点的深度为 1

这里以 Leetcode 定义为准

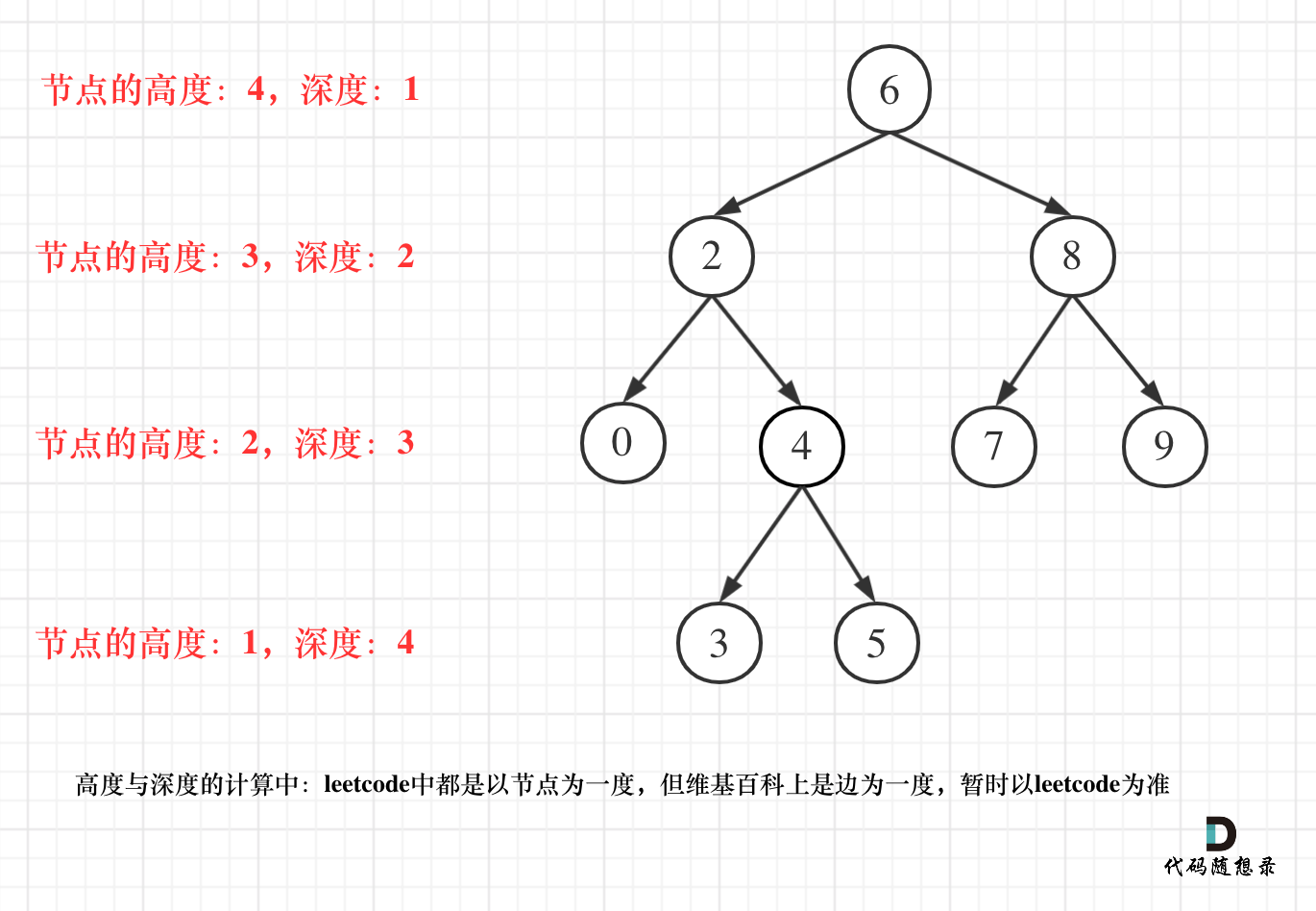
对于具有相同深度的节点，它们的高度不一定相同，这取决于它们下面的叶结点的深度

计算节点的深度，按照从上往下的顺序去遍历子节点，需要采用前序遍历

计算节点的高度，按照从下往上的顺序去遍历，需要采用后序遍历

参考：代码随想录：二叉树节点的深度与高度

# 树的深度与高度

二叉树的深度：所有节点中最深节点的深度，即，二叉树最底层节点的深度

二叉树的高度：根节点的高度

二叉树的 深度 与 高度 在数值上相等

因此，计算二叉树的深度（高度），可按照从上往下的顺序（前序遍历、层序遍历）计算最底层节点的深度，也可按照从下往上的顺序（后序遍历）计算根节点的高度

# 思路

按照本题的提示 “若每个节点的左子树与右子树的高度差不超过 1 ，该二叉树为平衡二叉树” ，可以通过计算每个节点左右子树的高度差来判断是否为平衡二叉树

一棵二叉树为平衡二叉树，当且仅当其所有子树都是平衡二叉树

因此，可以使用递归来判断。其中，递归可以按照 自顶向下 的顺序，也可以按照 自底向上 的顺序

# Method 1: 自顶向下

算法思路：

1. 定义一个递归函数 height ，用于计算节点 root 的高度
2. 从根节点开始遍历节点
   • 分别调用 height 函数计算左、右子树的高度
   • 若左右子树的高度差的绝对值大于 1，二叉树不是平衡二叉树，返回 false
   • 若左右子树的高度差的绝对值不超过 1，分别递归到左、右子节点（分别判断以左子节点为根节点、以右子节点为根节点的二叉树是否为平衡二叉树）

代码实现：

int height(TreeNode* root) { // 计算 root 节点的高度

    if (root == nullptr) return 0;

    return 1 + max(height(root->left), height(root->right));

}

bool isBalanced(TreeNode* root) { // 判断以 root 为根节点的树是否为平衡二叉树

    if (!root) return true;

    if (abs(height(root->left) - height(root->right)) > 1) //root 左右子树的高度差大于 1

        return false;

    return isBalanced(root->left) && isBalanced(root->right); // 递归到左右子节点

}

时间复杂度：$O(n^2)$，其中 $n$ 是二叉树的节点数

• 最坏情况下，二叉树为满二叉树，需要遍历满二叉树的所有节点，时间复杂度为 $O(n)$
• 对于任意节点 p ，如果它的高度为 $d$ ，则 height(p) 最多会被调用 $d$ 次（被 p 及其祖先节点调用），因此节点 p 的计算时间复杂度为 $O(d)$，其中，$d \le h$，$h$ 是二叉树的最大高度
  • 平均情况下，$O(h) = O(\log{n})$，此时，总的时间复杂度为 $O(n \log{n})$
  • 最坏情况下，二叉树呈链状，$O(h) = O(n)$，此时，总的时间复杂度为 $O(n^2)$

空间复杂度：$O(1)$，不考虑递归调用栈

# Method 2: 自底向上

注意，在上述方法中，对于每个节点， height 函数会被调用多次，故而时间复杂度较高

可以采用自底向上的顺序，对于每个节点， height 函数仅被调用 1 次

算法思路：

1. 定义 height 函数，输入参数为 root ，返回参数为 int 型的数

   • 分别递归到左子树、右子树（即，调用 height(root->left) 和 height(root->right) ），并记录其返回值
   • 判断左子树、右子树是否平衡
     • 若否，返回 -1
   • 判断以当前 root 节点为根节点的树是否平衡
     • 若是，返回 root 的高度
     • 否则，返回 -1

2. 若 height 函数返回值为 -1 ，二叉树不是平衡二叉树， isBalanced 函数返回 false

代码实现：

int height(TreeNode* root) { // 若二叉树为平衡二叉树，返回 root 的高度；否则，返回 -1

    if (!root) return 0;

    int leftHight = height(root->left);

    int rightHight = height(root->right);

    if (leftHight == -1 || rightHight == -1 || abs(leftHight - rightHight) > 1) // 非平衡

        return -1; // 返回 -1

    return 1 + max(leftHight, rightHight); // 平衡，返回高度

}

bool isBalanced(TreeNode* root) {

    if (height(root) == -1) return false;

    return true;

}

时间复杂度：$O(n)$，其中，$n$ 为二叉树的节点数

• 最坏情况下，需要遍历二叉树的所有节点，时间复杂度为 $O(n)$
• 每个节点仅计算一次高度，只进行一次 是否平衡 的判断，时间复杂度为 $O(1)$

空间复杂度：$O(1)$，不考虑递归调用栈

参考：力扣官方题解：平衡二叉树

# LeetCode 111. 二叉树的最小深度

LeetCode 111. Minimum Depth of Binary Tree

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 $[0, 10^5]$ 内
• $-1000 \le$ Node.val $\le 1000$

# 思路

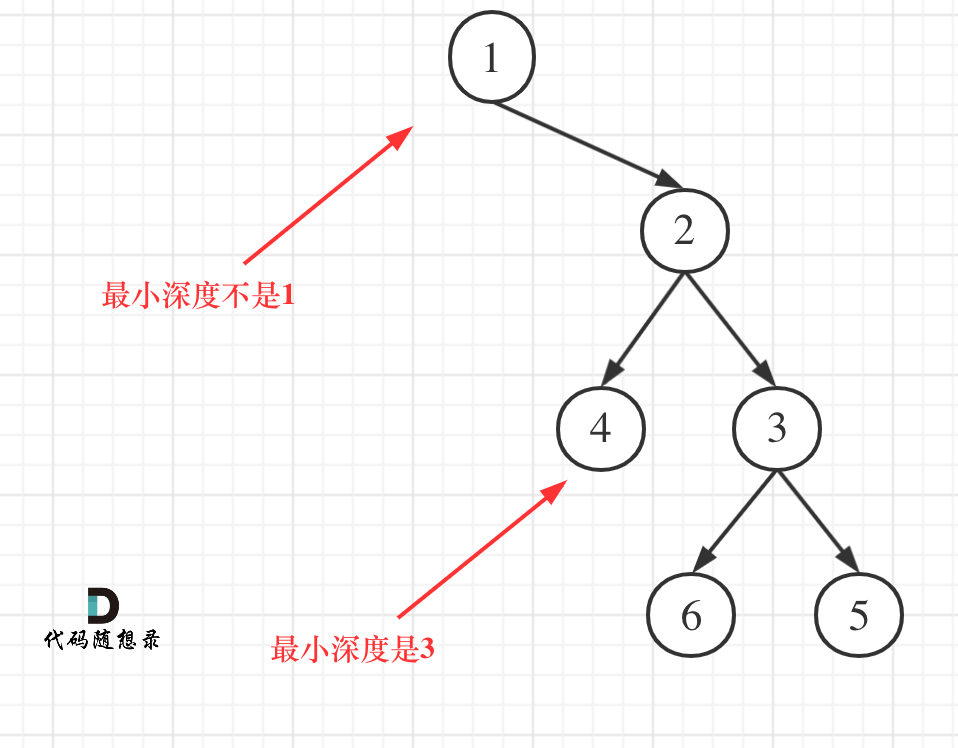
最小深度：从根节点到最近叶节点的最短路径上的节点数量

注意：叶节点是指左右子节点均为空的节点

参考：代码随想录：二叉树的最小深度

# Method 1: 递归

递归函数：

• 输入参数： root
• 函数返回值：以 root 为根节点的树的最小深度

# 写法一

递归终止条件：

• 若左子树与右子树均不为空，返回 1 + min (左子树最小深度、右子树最小深度)

• 若左子树为空、右子树不为空，返回 1 + 右子树的最小深度

• 若左子树不为空、右子树为空，返回 1 + 左子树的最小深度

• 若右子树与右子树均为空，节点为叶节点，返回 1

其中，第四种情况可与第二种（或，第三种）情况合并

代码实现：

int minDepth(TreeNode* root) {

    if (!root) return 0;

    if (!root->left) return 1 + minDepth(root->right);           // 左子树为空（包括左右子树均为空的情形）

    if (!root->right) return 1 + minDepth(root->left);           // 右子树为空

    return 1 + min(minDepth(root->right), minDepth(root->left)); // 左右子树均不为空

}

# 写法二

代码实现：

int minDepth(TreeNode* root) { // 返回 root 到叶节点的最小深度

    if (root == nullptr) return 0;

    int left = minDepth(root->left);   // 左子树最小深度

    int right = minDepth(root->right); // 右子树最小深度

    if (!left || !right)               // 左子树为空，或，右子树为空，最小深度为 1 + left + right

        return 1 + left + right;

    return 1 + min(left, right);       // 左子树与右子树非空，最小深度为 1 + min (left, right)

}

时间复杂度：$O(n)$，其中，$n$ 为二叉树的节点数

空间复杂度：$O(h)$，其中，$h$ 为二叉树的最大深度（这里考虑了递归时栈空间的开销）

• 最坏情况下，树呈现链状，空间复杂度为 $O(N)$
• 平均情况下，树的高度与节点数的对数正相关，空间复杂度为 $O(\log{N})$

参考：reals：二叉树的最小深度 - 理解递归结束条件

# Method 2: 层序遍历

算法思路：

• 逐层遍历，每层按从左到右顺序遍历
• 若遇到叶节点（即，左右子节点均为空），则返回当前遍历到的层数

代码实现：

int minDepth(TreeNode* root) {

    int ans = 0;

    queue<TreeNode*> que;

    if (root) que.push(root);

    while (!que.empty()) {

        ans++;

        int size = que.size();

        for (int i = 0; i < size; i++) {

            TreeNode* tmp = que.front();

            que.pop();

            if (tmp->left == nullptr && tmp->right == nullptr) return ans; //tmp 为叶节点

            if (tmp->left) que.push(tmp->left);

            if (tmp->right) que.push(tmp->right);

        }

    }

    return ans;

}

时间复杂度：$O(n)$，其中，$n$ 为二叉树的节点数

空间复杂度：$O(n)$

# LeetCode 112. 路径总和

112. Path Sum

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：false
解释：不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

• 树中节点的数目在范围 $[0, 5000]$ 内
• $-1000 \le$ Node.val $\le 1000$
• $-1000 \le$ targetSum $\le 1000$

# Method 1: 递归

hasPathSum 函数的功能：判断是否存在从当前节点 root 到叶节点的路径，使得路径和为 targetSum

假定从根节点到当前节点的路径和为 val ，则问题可以转换为：判断是否存在一条从当前节点的子节点到叶节点的路径，满足其路径和为 targetSum - val

因此，可以利用递归来实现这一系列问题的求解

算法思路：

1. 确定递归的参数和返回值：

   • 参数：根节点 root ，期望的 root-to-leaf 路径和 sum
   • 返回值： bool 类型，表示是否找到可行路径（设定返回值是为了在遇到可行路径时就返回，不再继续递归）

2. 递归终止条件：遇到叶节点，当前递归结束

3. 单层递归的逻辑：

   • 若 root 是叶节点，判断当前路径是否满足条件
   • 若不是叶节点，分别递归到左、右子树（注意，传入的第二个参数为 sum - root->val ）

代码实现：

bool hasPathSum(TreeNode* root, int sum) {

    if (!root) return false;        // 空节点，递归返回

    if (!root->left && !root->right)

        return  root->val == sum;   // 若当前叶节点的值等于 sum，路径符合条件，返回 true

    return hasPathSum(root->left, sum - root->val) ||

            hasPathSum(root->right, sum - root->val); // 判断是否存在从子节点到叶节点路径和为 sum - root->val 的路径

}

时间复杂度：$O(n)$，其中 $n$ 是二叉树的节点数

空间复杂度：$O(n)$，这里考虑了递归使用的栈空间

本题也可以累加路径和，在遇到叶节点时，判断路径和是否与目标值相等，但那样比较麻烦，例如：LeetCode 提交记录

参考：

• 代码随想录：路径总和
• 力扣官方题解：路径总和

# LeetCode 113. 路径总和 II

113. Path Sum II

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

• 树中节点总数在范围 $[0, 5000]$ 内
• $-1000 \le$ Node.val $\le 1000$
• $-1000 \le$ targetSum $\le 1000$

# Method 1: 递归

算法思路：综合 LeetCode 257. 二叉树的所有路径 和 LeetCode 112. 路径总和 这两题的思想

递归函数的参数：

• TreeNode *root ：当前节点
• vector<int> path ：记录从二叉树根节点到当前节点的路径（注意，参数传递方式为值传递）
• int sum ：从当前节点到叶节点应满足的路径和（注意，参数传递方式为值传递）

为避免 getPaths 函数需要传入太多参数，特将 vector<vector<int>> ans 设置为全局变量（记录所有可行路径）

代码实现：

vector<vector<int>> ans;

void getPaths(TreeNode *root, vector<int> path, int sum) {

    if (!root) return;                 // 空节点，递归终止

    path.push_back(root->val);         // 更新路径

    if (!root->left && !root->right) { //root 为叶节点

        if (root->val == sum)          // 若当前值等于 sum ，路径符合要求，将其添加到 ans

            ans.push_back(path);

        return;

    }

    getPaths(root->left, path, sum - root->val);  // 递归到左子树（传入 sum - root->val）

    getPaths(root->right, path, sum - root->val); // 递归到右子树（传入 sum - root->val）

}

vector<vector<int>> pathSum(TreeNode* root, int targetSum) {

    vector<int> path;

    getPaths(root, path, targetSum);

    return ans;

}

时间复杂度：$O(n^2)$，其中 $n$ 是二叉树的节点数

• 在最坏情况下，树的上半部分为链状，下半部分为完全二叉树，并且从根节点到每一个叶节点的路径都符合要求
• 此时，路径数目为 $O(n)$ ，每一条路径的节点个数也为 $O(n)$ ，因此总的时间复杂度为 $O(n^2)$

空间复杂度：$O(n)$，栈空间的开销

参考：力扣官方题解：路径总和 II

# LeetCode 114. 二叉树展开为链表

114. Flatten Binary Tree to Linked List

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

• The number of nodes in the tree is in the range [0, 2000].
• -100 <= Node.val <= 100

进阶：Can you flatten the tree with O(1) extra space?

# Method 1: 暴力法

算法思路：

首先按照前序遍历顺序将二叉树节点依次存入队列中

队首到队尾的元素对应于所需构建的二叉树链表的首端和尾端（因为展开后的单链表与二叉树前序遍历顺序相同）

于是，依据队列中的元素重构二叉树即可：对于队列中的任意元素（记作 node ），其 left 指针应为空指针，right 指针应指向其在队列中的下一个元素

queue<TreeNode*> que; // 存放先序遍历结果

void traverse(TreeNode* root) { // 先序遍历

    que.push(root);

    if (root->left) traverse(root->left);

    if (root->right) traverse(root->right);

}

void flatten(TreeNode* root) {

    if (root == nullptr)return; // 二叉树为空

    traverse(root);             // 获取先序遍历序列

    root = que.front();

    que.pop();

    while (!que.empty()) {      // 构造链表

        root->left = nullptr;   // 注意这里需要将 left 指针置为空指针

        root->right = que.front();

        que.pop();

        root = root->right;

    }

}

时间复杂度：$O(n)$，其中 $n$ 是二叉树的节点数

空间复杂度：$O(n)$，考虑了存放二叉树前序遍历结果所需空间，不考虑递归所需栈空间

# Method 2: 递归

算法思路：

定义一个递归函数，用于将以 root 为根节点的二叉树展开成链表

单层递归的具体逻辑为：

• 将左子树展开成链表（为便于表述，记作 左子树链表）
• 将右子树展开成链表（为便于表述，记作 右子树链表）
• 拼接左子树链表与右子树链表
• 将拼接结果作为新的右子树，并将左子树置为空

其中，题目要求展开所得的单链表与二叉树前序遍历顺序相同（即，根 - 左 - 右），因此，需要将右子树链表拼接在左子树链表的后面。即，需要找到左子树链表的尾端，令其 right 指针指向右子树链表的首端

代码实现：

void flatten(TreeNode* root) {

    if (root == nullptr) return;

    flatten(root->left);         // 将左子树展开成链表

    flatten(root->right);        // 将右子树展开成链表

    TreeNode* tmp = root->right; // 备份右子树的根节点

    root->right = root->left;    // 将 root 的左子树修改为 root 的右子树

    root->left = nullptr;        //root 的左子节点置为空指针

    TreeNode* node = root;       //root 左子树与 root 右子树的拼接点（即，左子树链表的尾端）

    while (node->right != nullptr) {

        node = node->right;

    }

    node->right = tmp;           // 将 root 右子树链表拼接在 root 左子树链表上

}

时间复杂度：$O(n)$，其中 $n$ 是二叉树的节点数

空间复杂度：$O(1)$，不考虑递归所需栈空间

# LeetCode 116. 填充每个节点的下一个右侧节点指针

LeetCode 116. Populating Next Right Pointers in Each Node

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* next;

    Node() : val(0), left(NULL), right(NULL), next(NULL) {}

    Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}

    Node(int _val, Node* _left, Node* _right, Node* _next)
        : val(_val), left(_left), right(_right), next(_next) {}
};

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：

输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

示例 2：

输入：root = []
输出：[]

提示：

• 树中节点的数量在范围 $[0, 2^{12} - 1]$ 内
• $- 1000 \le$ Node.val $\le 1000$

进阶：

• 你只能使用常量级额外空间。
• 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

# Method 1: 层序遍历

类似于 LeetCode 102. 二叉树的层序遍历

算法思路：

• 逐层遍历、每层按从左到右顺序遍历，利用队列存放待访问的节点
• 在遍历过程中，将 节点的 next 指针 指向 同一层的后一个节点（即，指向 队列的下一个元素）

代码实现：

Node* connect(Node* root) {

    queue<Node*> que;

    if (root) que.push(root);

    while (!que.empty()) {

        int size = que.size();

        for (int i = 0; i < size; i++) {

            Node* cur = que.front();

            que.pop();

            if (i < size - 1) cur->next = que.front(); // 除最右侧节点外，每个节点的 next 指针均指向右侧节点

            if (cur->left) que.push(cur->left);

            if (cur->right) que.push(cur->right);

        }

    }

    return root;

}

时间复杂度：$O(n)$，其中 $n$ 是节点个数

空间复杂度：$O(n)$

# Method 2: 使用已建立的 next 指针

算法思路：

本题的二叉树为满二叉树，每一层的节点都是满的。针对满二叉树而言， next 指针的连接方式有两种类型：

• 所连接的两个节点具有共同的父节点

• 所连接的两个节点具有不同的父节点，但他们的父节点通过 next 指针连接

算法流程：

1. 定义 pre 指向根节点，即，令 pre = root

2. 遍历二叉树的每一层，即，执行以下循环，循环条件是 pre->left 不为空：

   • 定义 cur 指向 pre 所在层的节点，初始时指向 pre
   • 遍历 cur ，建立 cur 下一层节点的 next 指针：
     • 若 cur 的左子节点不为空，则右子节点必不为空，通过 cur->left->next = cur->right 连接 cur 的两个子节点
     • 若 cur 的左子节点不为空 且 cur 的 next 指针不为空，通过 cur->right->next = cur->next->left 连接 cur 的右子节点与 cur->next 的左子节点
     • cur 向右移动，即，更新 cur = cur->next
   • 完成当前层的连接后，进入下一层重复操作，即 pre 向下移动（更新 pre = pre->left ）

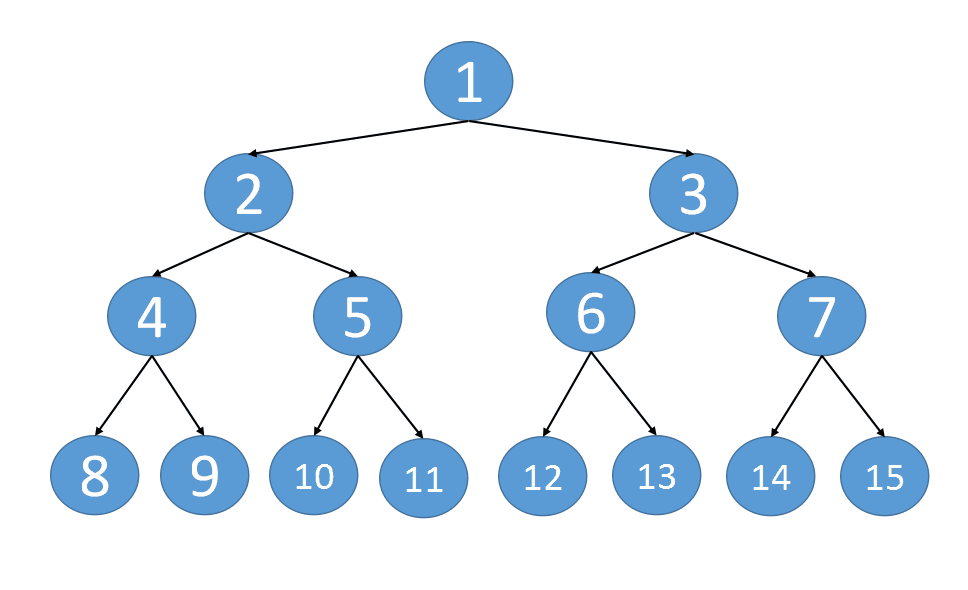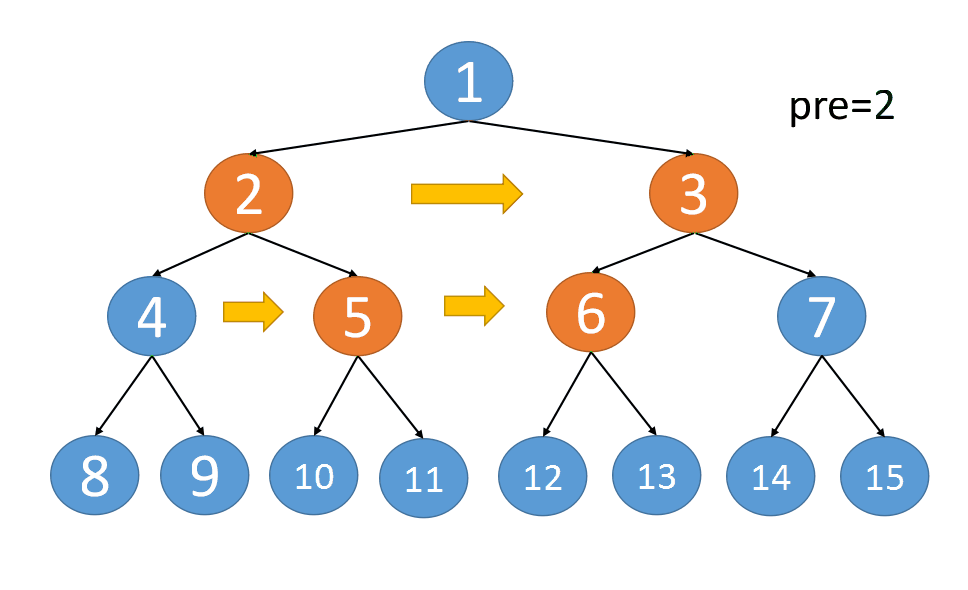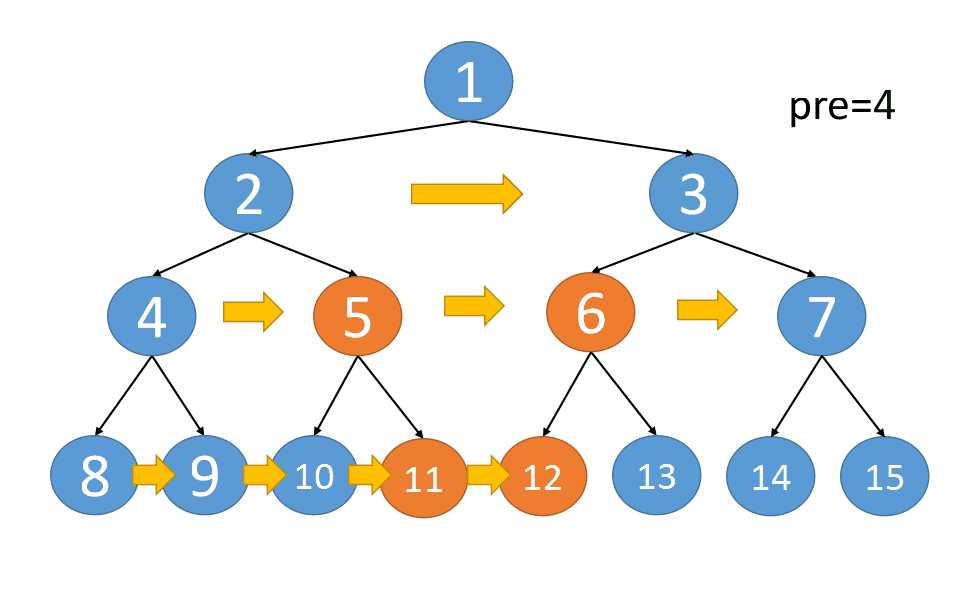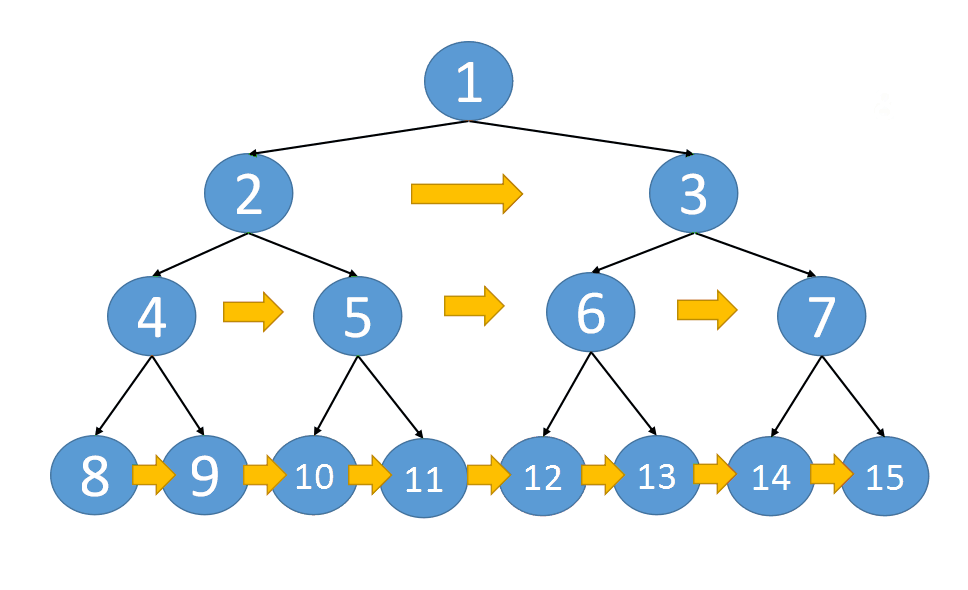
需要注意：

• pre 表示的是 pre 所在层的最左侧节点
• 遍历 cur 时， cur 所在层节点的 next 指针均已建立完成，此时建立的是下一层节点的 next 指针

代码实现：

Node* connect(Node* root) {

    if (root == nullptr) return root;

    Node* pre = root;

    while (pre->left != nullptr) { // 遍历二叉树的每一层

        Node* cur = pre;

        while (cur != nullptr) { // 遍历 pre 所在层的节点，建立下一层节点的 next 指针

                                 // 注意，外层的 while 循环已确保 cur 的下一层不为空

            cur->left->next = cur->right;           // 连接同一个父节点的两个子节点

            if (cur->next != nullptr)

                cur->right->next = cur->next->left; // 连接不同父节点之间子节点

            cur = cur->next;     // 向右移动

        }

        pre = pre->left;         // 向下一层移动

    }

    return root;

}

时间复杂度：$O(n)$，每个节点只访问一次

空间复杂度：$O(1)$，不需要额外空间用于存储

以上算法可改写成递归算法（即，深度优先搜索）

递归法的代码实现：

void DFS(Node* root) { // 更新 root 左右子节点的 next 指针

    if (root == nullptr || root->left == nullptr) return;

    root->left->next = root->right;

    if (root->next != nullptr)

        root->right->next = root->next->left;

    DFS(root->left);

    DFS(root->right);

}

Node* connect(Node* root) {

    DFS(root);

    return root;

}

参考：

• 代码随想录
• 力扣官方题解
• wang_ni_ma：动画演示 + 三种实现

# LeetCode 117. 填充每个节点的下一个右侧节点指针 II

LeetCode 117. Populating Next Right Pointers in Each Node II

给定一个二叉树：

struct Node {
    int val;
    Node *left;
    Node *right;
    Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：

输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

示例 2：

输入：root = []
输出：[]

提示：

• 树中的节点数在范围 $[0, 6000]$ 内
• $-100 \le$ Node.val $\le 100$

进阶：

• 你只能使用常量级额外空间。
• 使用递归解题也符合要求，本题中递归程序的隐式栈空间不计入额外空间复杂度。

# 思路

与 LeetCode 116. 填充每个节点的下一个右侧节点指针 不同，本题并未限定二叉树为满二叉树

因此，针对每个节点，都需在其右侧寻找距离其最近的节点

# Method 1: 层序遍历

算法思路：与 LeetCode 116. 填充每个节点的下一个右侧节点指针 的 Method 1 相同，利用队列存放待访问的节点，在二叉树每一层的访问完成之前，队列下一个元素即为当前元素 next 指针应指向的对象

该算法与 二叉树是否为满二叉树 无关

代码实现：

Node* connect(Node* root) {

    queue<Node*> que;

    if (root) que.push(root);

    while (!que.empty()) {

        int size = que.size();

        for (int i = 0; i < size; i++) {

            Node* cur = que.front();

            que.pop();

            if (i < size - 1) cur->next = que.front();

            if (cur->left) que.push(cur->left);

            if (cur->right) que.push(cur->right);

        }

    }

    return root;

}

时间复杂度：$O(n)$，其中 $n$ 是节点个数

空间复杂度：$O(n)$

# Method 2: 使用已建立的 next 指针

算法思路：

• 与 LeetCode 116. 填充每个节点的下一个右侧节点指针 的 Method 2 类似，可以利用已经建立了的 next 指针：即，在遍历 cur 的过程中，与 cur 处于同一层的各个节点的 next 指针均已建立完成，需要建立的是 cur 下一层节点的 next 指针

• 不同的是，由于二叉树不一定为满二叉树， cur 不一定存在左、右子节点，如果存在的话， cur->left 、 cur->right 应分别指向 cur->left 右侧的第一个节点、 cur->right 右侧的第一个节点，如 示例 1 所示

• 由于 pre 不一定具有左子节点，在更新 pre 时，不能简单地令 pre = pre->left ，需要对 pre 下一层的节点情况进行判断，更准确地说，需要找到 pre 下一层的最左侧节点，将其作为新的 pre

因此，本题在 LeetCode 116. 填充每个节点的下一个右侧节点指针 的基础上，作出以下改变：

• 定义 leftmost 指向 pre 下一层的最左侧节点

• 定义一个 handle 函数，在 root 右侧找到第一个非叶节点，返回其左子节点（不存在左子节点时，则返回右子节点）

  • 该函数用于确定 cur->left （不存在 cur->right 时）、 cur->right 的 next 指针的方向，也用于 leftmost 的更新

代码实现：

Node* handle(Node* root) { // 寻找 root 右侧第一个非叶节点的子节点（靠左侧的子节点）

    Node* cur = root->next;

    while (cur != nullptr) {

        if (cur->left) return cur->left;

        if (cur->right) return cur->right;

        cur = cur->next;

    }

    return nullptr;

}

Node* connect(Node* root) {

    if (root == nullptr) return root;

    Node* pre = root;

    Node* leftmost = pre->left ? pre->left : pre->right; //pre 下一层的最左侧节点

    while (leftmost != nullptr) {  // 当 pre 不是叶节点时执行循环

        Node* cur = pre;

        while (cur != nullptr) {

            if (cur->left)   // 当 cur 存在左子节点时，其 next 指针指向 cur->left 右侧第一个节点

                cur->left->next = cur->right ? cur->right : handle(cur);

            if (cur->right)  // 当 cur 存在右子节点时，其 next 指针指向 cur->right 右侧第一个节点

                cur->right->next = handle(cur);

            cur = cur->next; //cur 向右移动

        }

        pre = leftmost;      //pre 向下移动：更新 pre 为 leftmost

        if (pre->left)       // 更新 leftmost

            leftmost = pre->left;

        else if (pre->right)

            leftmost = pre->right;

        else

            leftmost = handle(pre);

    }

    return root;

}

时间复杂度：$O(n)$，其中 $n$ 是节点个数，每个节点至多被访问 3 次

• 确定 cur->left 和 cur->right 的 next 指针时，至多访问 cur 右侧各个节点 1 次
• 遍历 cur 时，访问各节点 1 次
• 更新 leftmost 时，至多访问 pre 下一层的各个节点 1 次

空间复杂度：$O(1)$

注意，本题的样例并不一定为满二叉树，不能将该算法改写成递归法（深度优先搜索）。因为在调用 handle 时，与 root 同一层节点的 next 指针可能并未更新完成，这将导致 handle 函数返回错误结果

与 Method 1 相比，Method 2 的时间复杂度相对较高，空间复杂度相对较低

# Method 3: 链表

可以将二叉树的每一层都看成一个链表

算法流程：

1. 定义：指针 dummyHead 指向虚拟头节点，指针 cur 指向当前遍历到的二叉树节点，指针 LinkedNode 指向链表的当前节点

2. 当 cur 不为空时，执行循环：

   • 令 LinkedNode = dummyHead
   • 在同一层上遍历 cur ：
     • 若 cur 的左子节点不为空，将左子节点串进链表，并更新 LinkedNode
     • 若 cur 的右子节点不为空，将右子节点串进链表，并更新 LinkedNode
     • 继续访问这一层的下一个节点
   • 更新 cur 为下一层的最左侧节点，即， cur = dummyHead->next
   • 重置哑结点 dummyHead 的 next 指针，即， dummyHead->next = nullptr

在内层的循环中，遍历的是 cur 所在层的节点，串联的是 cur 下一层的节点

代码实现：

Node* connect(Node* root) {

    if (root == nullptr) return root;

    Node* cur = root;              // 当前节点

    Node* dummyHead = new Node();  // 链表的哑结点（定义在最外层，确保空间复杂度为 O (1)）

    Node* LinkedNode = nullptr;    // 链表的当前节点